Solution Solution provided by AtoZmathcom Substitution Method Solve Linear Equation in Two Variables Solve linear equation in two variables 1 12x 5y = 7 and 2x 3y 5 = 0 2 x y = 2 and 2x 3y = 4 3 7y 2x 11 = 0 and 3x y 5 = 0SUBSTITUTION METHOD EXAMPLES The following steps will be useful to solve the systems of linear equations using substitution Step 1 In the given two equations, solve one of the equations either for x or y Step 2 Substitute the result of step 1 into other equation and solve for the second variable Step 3Solve for x x in the first equation Tap for more steps Move all terms not containing x x to the right side of the equation Tap for more steps Add 1 1 to both sides of the equation Add 3 3 and 1 1 Divide each term by 2 2 and simplify Tap for more steps Divide each term in 2 x = 4 2 x

Solve The Following Pair Of Linear Equation By Substitution Method I X Y 2 3x 2y 16 Brainly In
X-y=3 x/3+y/2=6 by substitution method
X-y=3 x/3+y/2=6 by substitution method-Solve for x and y, using substitution method ` 2x y = 7, 4x 3y 1 =0 `You can put this solution on YOUR website!




Ex 3 3 1 Solve By Substitution Method I X Y 14 Ex 3 3
Substitution method can be applied in four steps Step 1 Solve one of the equations for either x = or y = Step 2 Substitute the solution from step 1 into the other equation Step 3 Solve this new equation Step 4 Solve for the second variableAubrey is using the substitution method to solve the following system of equations y − x = 21 2y = 2x 16 She arrives at an answer of 8 = 21 She thinks that this answer means that the lines are parallel and that the system has no solutionHere are the Steps using Substition method 1 In either equation, solve for one variable in terms of the other We are going to solve for y in terms of x xy=12 y = x12 2 Substitute x12 for y in the other equation x3/2y=3/2 Solve x, y = x12 x = 33 3 Substitute the result from step 2 in either equation Solve for the other variable y
Solve by Substitution Calculator Step 1 Enter the system of equations you want to solve for by substitution The solve by substitution calculator allows to find the solution to a system of two or three equations in both a point form and an equation form of the answer Step 2 Click the blue arrow to submitSolve by Substitution y=x6 y=2x3 y = x 6 y = x 6 y = −2x − 3 y = 2 x 3 Eliminate the equal sides of each equation and combine x6 = −2x−3 x 6 = 2 x 3 Solve x6 = −2x−3 x 6 = 2 x 3 for x x Tap for more steps Move all terms containing x x to the left side of the equation One way is to use the method of elimination Step 1 Enter the equations 1 y = x2 3x 2 y = 6 −2x Step 2 Solve for one of the variables in terms of the other 2 y = 6 −2x Since this is already done for us, we can go on to the next step
Let's first solve for 'y' in the 1st equation, then substitute that into 2nd equation 2x y = 3 ==> y = 3 2x 4x y 3 is not an equation, so let's assume you meant 4x y = 3 4x y = 3 ==> 4x (3 2x) = 3 ==> 2x = 6 ==> x = 3 Place x = 3 back into either equation to find 'y', use the 1st equation, for example 2x y = 3 ==> 2 (3) y = 3 ==> y = 9(a) 2x 3y = 12(i) and x y = 1(ii) (ii)×3 ==> 3x 3y = 3(iii) Now we can eliminate y by adding (i) & (iii) (i) (iii) ==> 5x = 15 so x=3 Transcript Ex 33, 1 Solve the following pair of linear equations by the substitution method (i) x y = 14 x – y = 4 x y = 14 x – y = 4 From equation (1) x y = 14 x = 14 – y Substituting value of x in equation (2) x – y = 4 (14 – y) – y = 4 14 – y – y = 4 14 – 2y = 4 –2y = 4 – 14 –2y = –10 y = (−10)/(−2) y = 5 Putting y = 5 in (2) x – y = 4 x = y 4 x



The Substitution Method




Ex 3 4 1 Solve By Elimination And Substitution I X Y 5 2x 3y
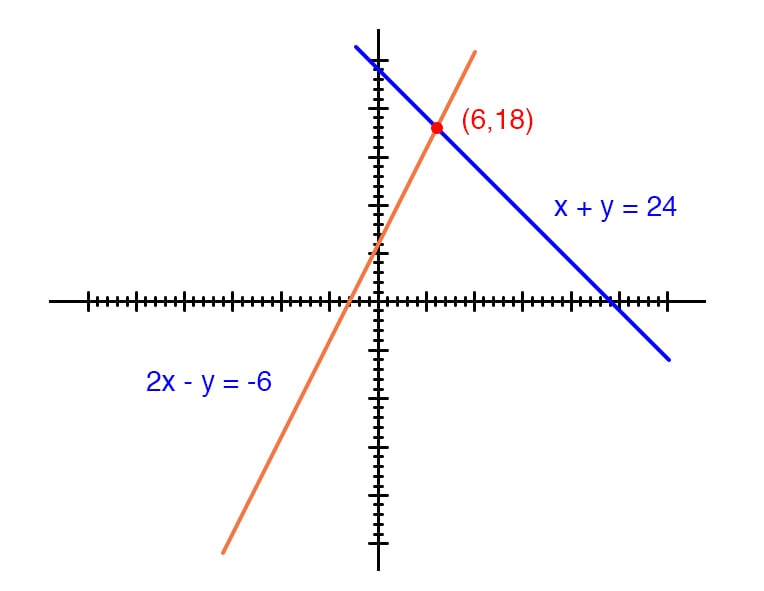
Solve the following pair of linear equations by the substitution method (3x)/2 (5y)/3 = 2, x/yy/2 = 13/6 How do you solve #12y3x=1# and #x4y=1# using the substitution method?By substitution method x y =5 (1) subtract y both side we get x = 5 y ,(4) plug the value of x in equation second we get 2(5 – y ) – 3y = 45y = 6 y = 6/5 = 6/5 Plug the value of y in equation 4 we get x = 5 – 6/5 x = 19/5




1 Topic The Substitution Method 2 Topic The Substitution Method California Standard 9 0 Students Solve A System Of Two Linear Equations Ppt Download




1 Solve The Following Pair Of Linear Equations By The Substitution Method 1 X Y 14 Ii S T 3 S 6 X Y 4 Ii 3x Y 3 9x 3y 9 3 2 Iv 0 2x 0 3y 1 3 0 4x
3x/2 5y/3 = 2 and x/3y/2=13/6 Solve using substitution methodQuestion 2 Substitution Method Xy=16 And Y=3x 3 Solve The System By The Substitution Method Y= 2x 7 And 2x 3y = 19 4 Xy= 1 And Xy= 5 Solve The System By The Addition Method 5 Solve The System By The Addition Method 4x13y= 8 And 2x13y=4 6 Solve The System By Graphing 3x2y=12 And X 2y= 4 Explanation 2x 3y = 6 x y = 3 Let's solve for x in the second equation x = 3 −y Now let's plug (3 − y) in for x in the first equation 2(3 −y) 3y = 6 6 − 2y 3y = 6 y = 0




Solve The Following System Of Equations 27 X Y 15 X Y 2 And 30 X Y 1 X Y 3 Mathematics Topperlearning Com X68shsoo



Solved Find The Common Solution Of Each Using The Elimination Substitution And Graphical Method 2x Y 2 X 3y 36 2 3x Y 6 X Y 6 3 Course Hero
Use the Substitution method to solve the system of equations y 2x = 5 3y x = 5 Solve one of the equations for x or y Let's solve the first one for y y 2x = 5 y = 2x 5 Now let's substitute 2x 5 for y in the second equation to solve for x 3(2x 5) x = 5 6x 15 x = 5 5x 15 = 5 5x = x = 4 Substitute 4 for x in either equation to solve for y Let's choose the first one yClick here to see ALL problems on Linearequations Question 6702 Solve the following system using substitution x3y=8 2xy=2 Answer by jim_thompson5910 () ( Show Source ) You can put this solution on YOUR website!Question solve using the substitution method y = 3 x 2x 4y = 6 Answer by jim_thompson5910() (Show Source) You can put this solution on YOUR website!




Exercise 33 1 Solve The Follo See How To Solve It At Qanda




3 Systems Of Linear Equations
Substitution Method Use the Substitution method to solve the system of equations x y = 4 x y = 2 x y = 4 x y = 2 In the second equation, x= y2 Putting that in the first (y2) y= 4 subtract two from each side, then divide each side by Solve the following pair of linear equations by substitution method x y = 2m;Solve by Substitution 2xy=3 , xy=0 2x − y = −3 2 x y = 3 , x y = 0 x y = 0 Subtract y y from both sides of the equation x = −y x = y 2x−y = −3 2 x y = 3 Replace all occurrences of x x with −y y in each equation Tap for more steps Replace all occurrences of x x in 2 x − y = − 3 2 x y = 3 with − y
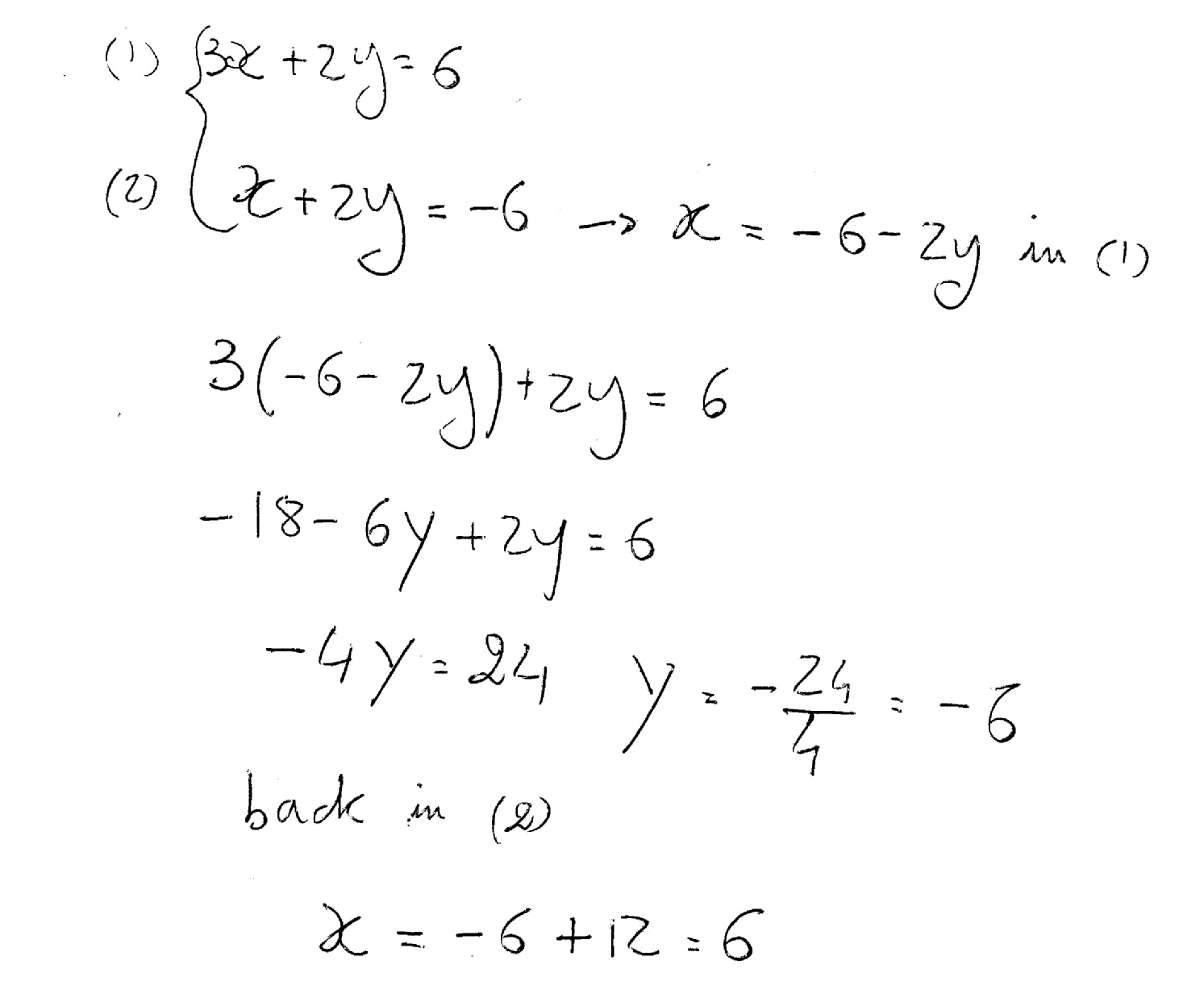



How Do You Solve By Substitution 3x 2y 6 And X 2y 6 Socratic




Systems Of Equations With Substitution 2y X 7 X Y 4 Video Khan Academy
xy=3=> x=y3 x/3 y/2=6 Substituting in ( x/3y/2=6) => (y3)/3y/2=6 => (2y63y)/6=6 =>2y63y=36 =>5y=30 => y=5 Substituting (y= 5)in xy=3Answer to Solve the system by the method of substitution x = y 3 x = y^2 1 By signing up, you'll get thousands of stepbystep solutionsFind an answer to your question xy=33 06/3x2y=1 solve this by substitution method Plsss




Q 1 2x 5y Xy 6 4x 5y Xy 3 Solve By Substitution Method Q 2 X 3 Y 4 11 5x 6 Y 3 7 0 Solve By Substitution Answer Fast Plz Maths Pair Of Linear Equations In Two Variables




X Y 3x 7 X Y 2x 11 Novocom Top
What are the 2 numbers if the sum is 70 and they differ by 11?Askedin Mathematicsby Samantha(3kpoints) Solve the following pairs of linear equations by the substitution method 3x/2 5y/3 = 2, x/3 y/2 = 13/6 pair of linear equations in two variables cbse class10Which method do you use to solve the system of equations #y=1/4x14# and #y=19/8x7#?



Solve The Following Systems Of Equations 6 X Y 7 X Y 3 1 2 X Y 1 A X Y Where X Y 0 And X Y 0 Sarthaks Econnect Largest Online Education Community




How Do You Solve The System 4x 2y 6 And X Y 3 Socratic
You have the equations of 2 coincident lines, or, two lines one superimposed over the other, so, your system will have ∞ solutions (ie, ∞ pointsIsolate xfrom equation (1), we get x=3−y Substituting the value of xin equation (2) 4(3−y)−3y=26 12−4y−3y=26 −7y=14 y=−2 Solve for x' x=3−y=3−(−2)=5Solve the following pairs of linear equations by the substitution method 02x 03y = 13, 04x 05y = 23 asked in Mathematics by Samantha ( 3k



How To Factorise 3 X Y 2 2 X Y Quora




Solve The Pair Of Linear Equations 2x 3y 12 And 3x 2y 13 By Elimination Method
Explanation Take the first equation and substitute into the second for x 2(3 −2y) 4y = 6 6−4y 4y = 6 6 = 6 !!! Solve the following system of equations by using the substitution method y = x 3 and y = 2x – 4Substitution Method xy = 5 and 2x3y = 4LinkedIn Profilehttps//wwwlinkedincom/in/arunmamidi8ba/FaceBookhttps//wwwfacebookcom/arunkumarm144




Systems Of Equations Substitution Method Ppt Video Online Download



Simultaneous Equations Gmat Math Study Guide
Start with the given system of equations Now in order to solve this system by using substitution, we need to solve (orClick here to see ALL problems on Linearequations Question Substitution method y=4x9 y=x3 Answer by sofiyac (9) ( Show Source ) You can put this solution on YOUR website!Mx ny = m^2 n^2 asked in Linear Equations by Anika01 (



How Do You Solve The System 2 X 4 Y 6 3x 2 Y 3 13 Socratic



The Substitution Method
x=2 and y=1 y=x1 xy=3 In the second equation, substitute y with its value from the first equation, color(red)((x1)) xy=3 xcolor(red)((x1))=3 Open the brackets and simplify xcolor(red)(x1)=3 2x1=3 Add 1 to each side 2x=4 Divide both sides by 2 x=2 In the first equation, substitute x with color(blue)2 y=x1 y=color(blue)21 y=1X y = 15;Answer to Solve using the substitution method 4x 2y = 6;



Cbse 10 Math Cbse Linear Equations In Two Variables Ncert Solutions



If X Y 2 Then What Is The Value Of X Y 6xy Quora
3xy=2_x3y=6 Since 3x does not contain the variable to solve for, move it to the righthand side of the equation by subtracting 3x from both sides y=3x2_x3y=6 Replace all occurrences of y with the solution found by solving the last equation for y In this case, the value substituted is 3x2Solve by substitution method x^2=y^239 xy=3 Math question Please help me to solve by substitution method 7x8y =44 x=415y math problem solve by substitution method 7x8y=44 x=415y college of the redwoods x9y=42 3x8y=50 solve using the substitution method AlgebraAnswer to Solve by using the substitution method y=3x2, \\ x=4 By signing up, you'll get thousands of stepbystep solutions to your homework
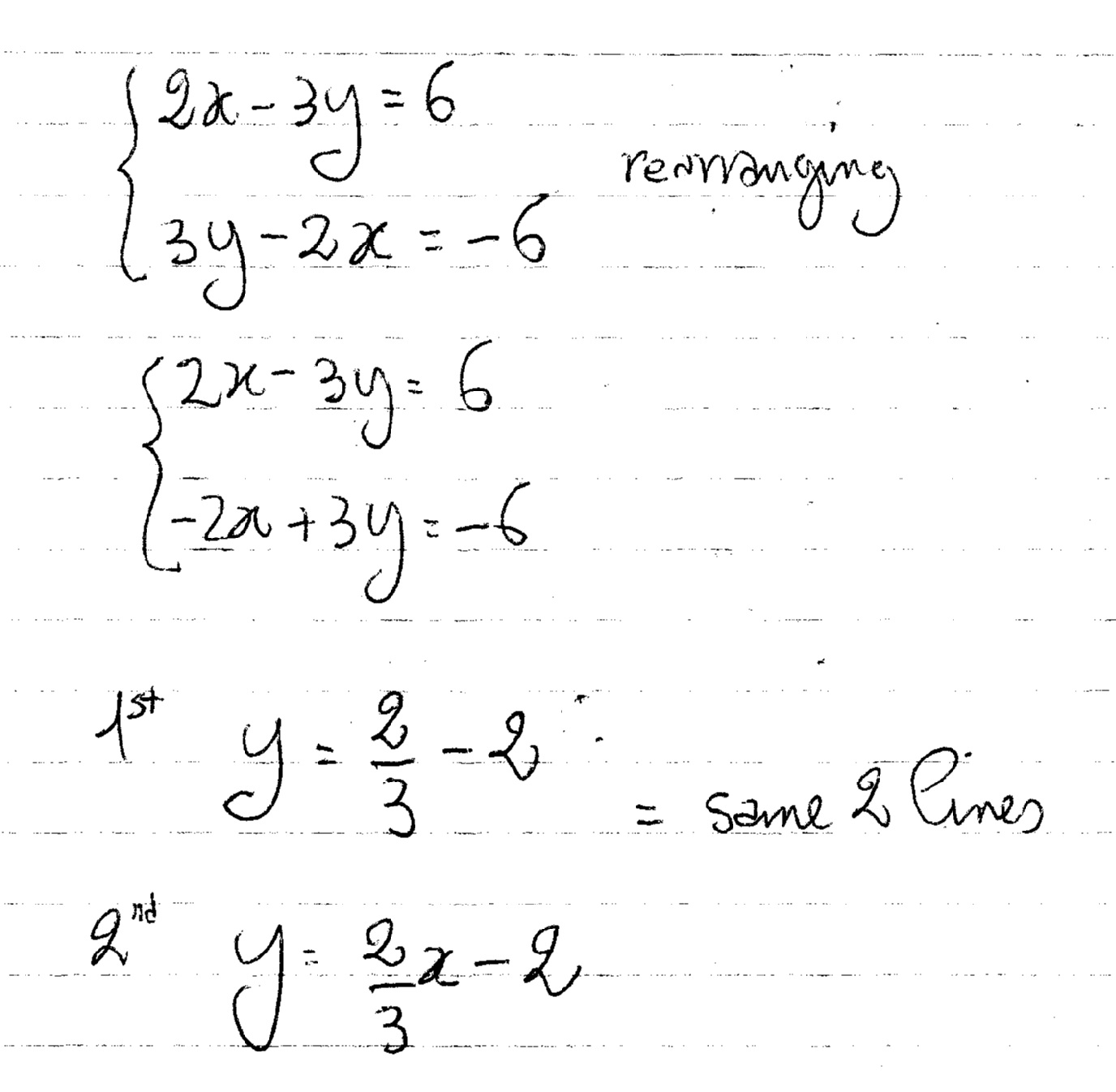



How Do You Solve The System Of Equations 2x 3y 6 And 3y 2x 6 Socratic




X 2 2y 3 1 Amp X Y 3 3 Solve By Eliminations Or Substitution Method Brainly In
In reality the second equation is equal to the first multiplied by 2 !!!Solving Systems of Equations Using Substitution Procedure (a) Use one of the equations in the system of equations to solve for one of the variables in terms of the other variables (b) Substitute the expression obtained in the previous step into the other equations, resulting in a new system of equations with one less variable and one lessX−y = 3 (1)xy = 0 (2)From equation 1 y = x−3Substitute the value of y in equation 2 xy = 0xx−3= 02x = 3X = 23 Now, Substitute x = 23 in equation 1x−y = 323 −y = 3y = 23 −3y = −23 Therefore the solution is x = 23 and y = −23




Solving Simultaneous Equations Equations And Inequalities Siyavula




Example 18 Solve 5 X 1 1 Y 2 2 6 X 1 3 Y 2 1 Examples
Click here 👆 to get an answer to your question ️ Solve, using the substitution method 3x 2y = 8 y = x – 6 leshia leshia Mathematics High School answered Solve, using the substitution method 3x 2y = 8 y = x – 6 1 See answer leshia is waiting for your help Add your answer and earn pointsCancel the common factor Divide y y by 1 1 Divide 3 3 by 3 3 Replace all occurrences of y y with 1 1 in each equation Tap for more steps Replace all occurrences of y y in x = y x = y with 1 1 Remove parentheses The solution to the system is theStart with the given system Plug in into the first equation In other words, replace each with




Solve The Following Pair Of Linear Equation By Substitution Method I X Y 2 3x 2y 16 Brainly In




6 2 Solving Systems Of Linear Equations 455 We Have Chegg Com
2x 3 = y By signing up, you'll get thousands of stepbystep solutions to yourX y = 3 Solve Using Substitution Method




Ex 3 3 1 Solve By Substitution Method I X Y 14 Ex 3 3




新しいコレクション Solve X Y 14 X Y 4 By Substitution Method Solve X Y 14 X Y 4 By Substitution Method Gasaktuntaslbgd




Solving Simultaneous Equations The Substitution Method And The Addition Method Algebra Reference Electronics Textbook



Systems Of Linear Equations




X Y 3 X 3 Y 2 6 Youtube




Solution Of X Y 3 And X 3 Y 2 6 By Elimination Method Brainly In




By Substitution Method Solve X 3 Y 4 6 X 6 Y 2 6 Brainly In




Let S Learn Solving Systems Using The Substitution Method




1 Solve The Following Pair Of See How To Solve It At Qanda




3 Systems Of Linear Equations




Solve The Following System Of Equations By Using The Method Of




Solve For X And Y 40 X Y 2 X Y 5 And 25 X Y 3 X Y 1 Mathematics Topperlearning Com Idbi1itt




X 3 Y 4 11 5x 6 Y 3 7 Solve In Substitution Method Brainly In




X 2 Y 2 3 6 Xy 12 Novocom Top



The Substitution Method




Ex 3 4 1 Solve By Elimination And Substitution I X Y 5 2x 3y



Solve 5 X 1 1 Y 2 2 And 6 X 1 3 Y 2 1 Studyrankersonline




Ex 3 3 1 Solve By Substitution Method I X Y 14 Ex 3 3
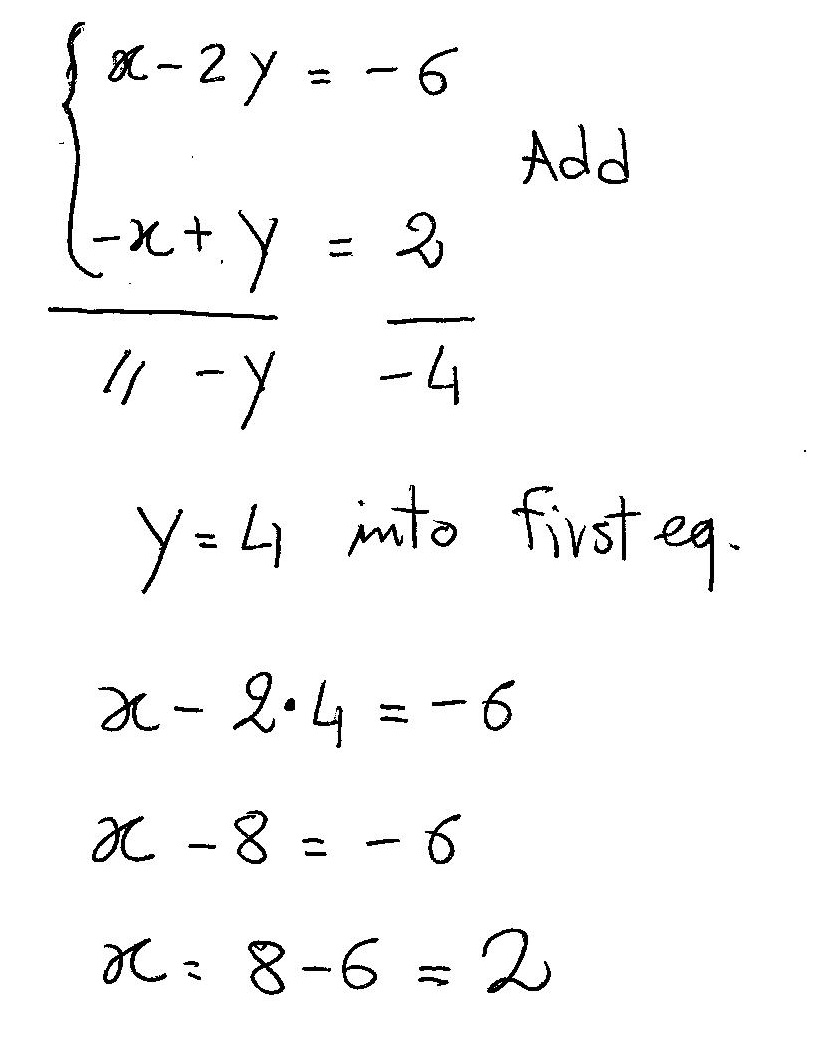



How Do You Solve X 2y 6 And X Y 2 Socratic




Ex 3 3 1 Solve By Substitution Method I X Y 14 Ex 3 3



Solve The Following Pairs Of Linear Equations By The Substitution Method 3x 2 5y 3 2 X 3 Y 2 13 6 Sarthaks Econnect Largest Online Education Community




Solve By Reducing Them To A Pair Of Linear Equations 5 X 1 1 Y 2 2 6 X 1 3 Y 2 1 Youtube




By Substitution Method Solve X 3 Y 4 6 X 6 Y 2 6 Brainly In




6 X Y 7 X Y 3 1 2 X Y 1 3 X Y




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3
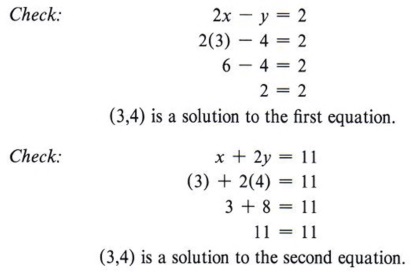



Graph Graph Inequalities With Step By Step Math Problem Solver




1 Solve The Following Pair Of See How To Solve It At Qanda
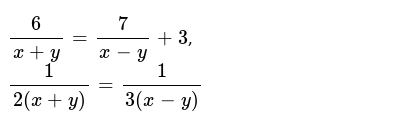



6 X Y 7 X Y 3 1 2 X Y 1 3 X Y



How To Solve For X And Y In X Y 5 And Xy 6 Quora




Warm Up Solve Each Equation For X 1 Y X Y 3x 4 Ppt Video Online Download




2 X Y 2 X 3 Y 15 Solve By Substitution Method Maths Meritnation Com




Ex 3 3 1 Solve By Substitution Method I X Y 14 Ex 3 3




Ncert Class 10 Mathematics Chapter Wise Questions And Answers And Solutions




Solve The Following Pair Of Linear Elimination Method And The Subs




Ml Aggarwal Solutions For Class 9 Maths Chapter 5 Simultaneous Linear Equations
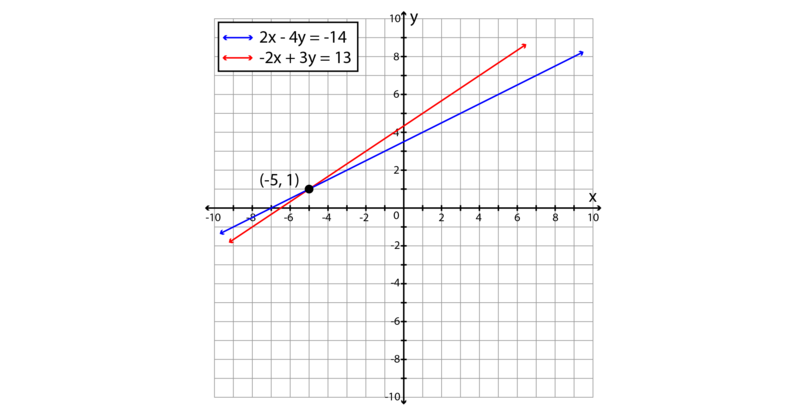



Substitution Method Simultaneous Linear Equations Siyavula



How Do You Solve The System 2 X 4 Y 6 3x 2 Y 3 13 Socratic




Graph Graph Inequalities With Step By Step Math Problem Solver




7 Y 3 2 X 2 14 4 Y 2 3 X 3 2 Youtube




Solve Equations Using Substitution Method 2x Y 3 And 4x Y 3



Solve The Following Systems Of Equations 6 X Y 7 X Y 3 1 2 X Y 1 A X Y Where X Y 0 And X Y 0 Sarthaks Econnect Largest Online Education Community
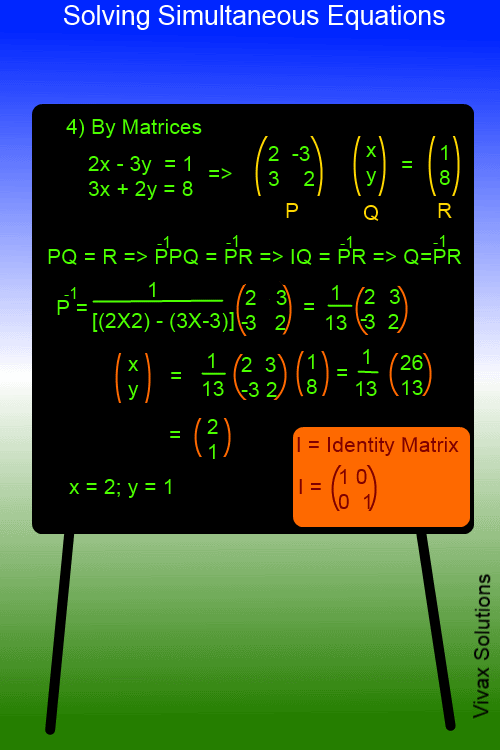



Solving Simultaneous Equations Elimination Substitution Graphical Matrix Methods Maths Tutorials Vivax Solutions




X 2 2y 3 1 And X Y 3 3 Find X And Y Values Using Elimination And Substitution Method Youtube
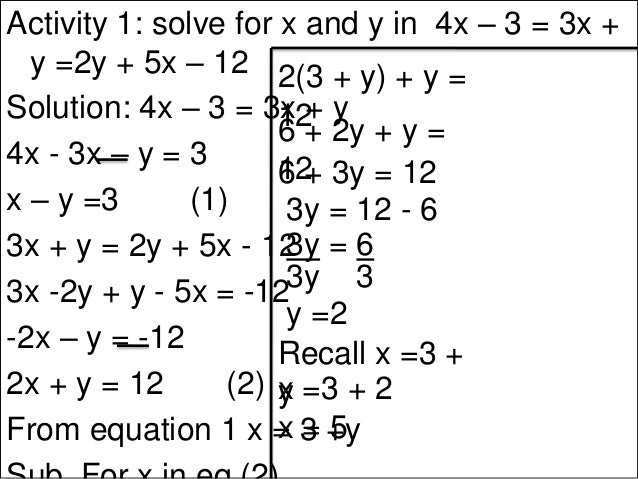



Simultaneous Equations




X 7 Y 3 5 X 2 Y 9 6 By Elimination Method Novocom Top




Cramer S Rule To Solve A System Of 3 Linear Equations Example 2 Youtube



Solving Simultaneous Equations The Substitution Method And The Addition Method Algebra Reference Electronics Textbook
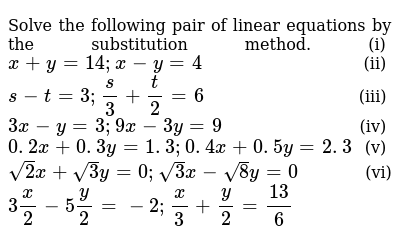



Solve The Following Pair Of Linear Equations By The Substitut



Graph Graph Inequalities With Step By Step Math Problem Solver




Solving Systems Of Equations With Fractions Or Decimals Video Lessons Examples And Solutions




Exercise 3a3 Solve The Follow See How To Solve It At Qanda



How To Solve These Simultaneous Equations X 3 2y X 2y 27 And 2x Xy Y 22 X Y 1 Quora




X Y 3 And X 3 Y 2 6 Solve The Following Pair Of Linear Equations By The Elimination Method And Brainly In




Answered Y 4 3 1 2 12x 10y 4 3 5 2 Bartleby
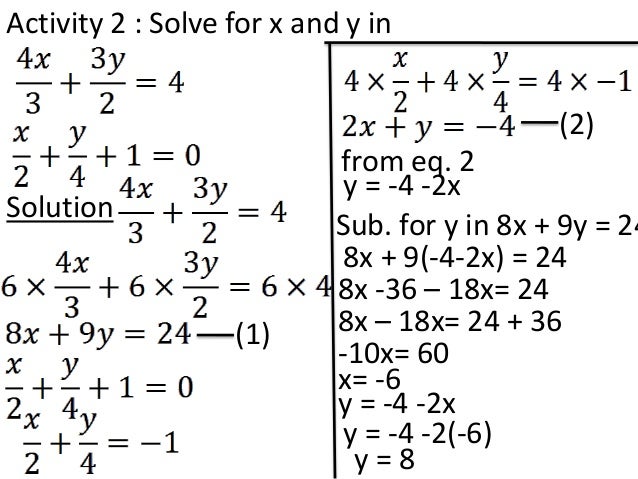



Simultaneous Equations




J19




Ex 3 3 1 Solve By Substitution Method I X Y 14 Ex 3 3



How To Solve The Following Simultaneous Equations By Elimination Method A 2x 3y 12 X Y 1 B 3x Y 10 C X 3y 1 3x 2y 4 0 D 5 Quora



Who Can Solve This X Y 15 And X Y 3 Find X And Y Quora




3x 2 5y 3 2 And X 3 Y 2 13 6 Solve Using Substitution Method Youtube



How To Solve For X And Y In X Y 5 And Xy 6 Quora




Systems Of Equations Substitution Method Ppt Video Online Download




Solve X Y 3 And X 3 Y 2 6 By Substituting Methos Scholr
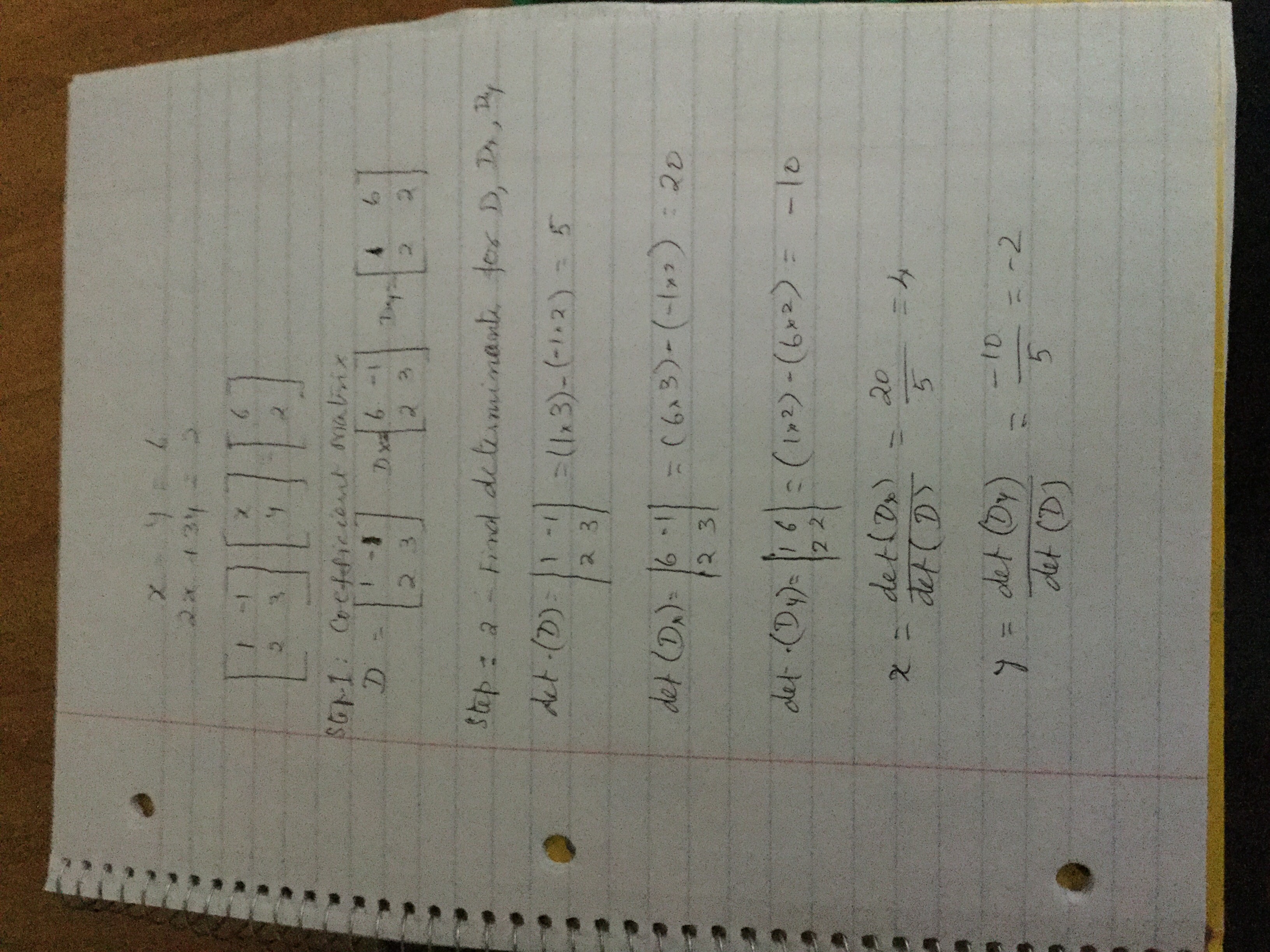



How Do You Solve X Y 6 And 2x 3y 2 Using Matrices Socratic



What Are X And Y From The System Equation 2x 3y 4 X Y 6 Quora



Link Springer Com Content Pdf m 3a978 1 349 3 2f1 Pdf




Graph Graph Inequalities With Step By Step Math Problem Solver




Exercise 33 1 Solve The Follo See How To Solve It At Qanda




X Y 3 X 3 Y 2 6




R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3




Chapter 5 Review Exercises




X 2 2y 3 1 And X Y 3 3 Solve By Elimination Method Brainly In



No comments:
Post a Comment