In mathematics, the logarithm is the inverse function to exponentiationThat means the logarithm of a given number x is the exponent to which another fixed number, the base b, must be raised, to produce that number xIn the simplest case, the logarithm counts the number of occurrences of the same factor in repeated multiplication; Ex 25, 7 Evaluate the following using suitable identities (i) (99)3 We write 99 = 100 – 1 (99)3 = (100 − 1)3 Using (a – b)3 = a3 – b3 – 3ab(a – b) Where a = 100 & b = 1 = (100)3 − (1)3 − 3(100) (1) (100 − 1) = − 1 − 300(99) = − 1 − = Ex 25, 7 Eva(a 3 3a 2 b 3ab 2 b 3)(ab) = a 4 4a 3 b 6a 2 b 2 4ab 3 b 4 The calculations get longer and longer as we go, but there is some kind of pattern developing That pattern is summed up by the Binomial Theorem

Qg0dbobeox2fsm
Expand (1/x+y/3)^3 class 9
Expand (1/x+y/3)^3 class 9- ML Aggarwal Class 9 Solutions for ICSE Maths Chapter 3 Expansions Chapter Test Question 1 Find the expansions of the following (i) (2x 3y 5) (2x 3y – 5)Class 9 RD Sharma Solutions Chapter 4 Algebraic Identities Ex 43 Question 1 Find the cube of each of the following binomial expressions Solution Question 2 If a b = 10 and ab = 21, find the value of a 3 b 3 Solution a b = 10, ab = 21




Rd Sharma Class 9th Solutions Chapter 1 Number Systems
Quotient of x^38x^217x6 with x3;👉 Learn all about sequences In this playlist, we will explore how to write the rule for a sequence, determine the nth term, determine the first 5 terms orTaylor series of a function is the sum of infinite series or infinite terms Taylor series is polynomial of sum of infinite degree It is used in various fields such as calculus Maclaurin Series Expansion
(),where f (n) (a) denotes the n th derivative of f evaluated at the point aBrainlycom For students By students Brainly is the place to learn The world's largest social learning network for students Explanation (x −y)3 = (x − y)(x −y)(x −y) Expand the first two brackets (x −y)(x − y) = x2 −xy −xy y2 ⇒ x2 y2 − 2xy Multiply the result by the last two brackets (x2 y2 −2xy)(x − y) = x3 − x2y xy2 − y3 −2x2y 2xy2 ⇒ x3 −y3 − 3x2y 3xy2 Always expand each term in the bracket by all the other
Write expression log(x4y7 z16) log ( x 4 y 7 z 16) as a sum or difference of logarithms with no exponents Simplify your answer completely log(x4y7 z16) = log ( x 4 y 7 z 16) = Get help Box 1 Enter your answer as an expression Example 3x^21, x/5, (ab)/c Be sure your variables match those in the questionCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyPhone support is available MondayFriday, 900AM1000PM ET You may speak with a member of our customer support team by calling End of Conversation Have a great day!




Selina Solutions For Concise Mathematics Class 9 Icse Chapter 4 Expansions Including Substitution Latest Edition Shaalaa Com




Please Expand 1 X Y 3 Whole Cube Brainly In
This calculator can be used to expand and simplify any polynomial expressionShare It On Facebook Twitter Email 1 Answer 0 votes answered by Atthar (434k points) selected by Maniraj Best answer Correct Answer CML Aggarwal Solutions for Class 9 Maths Chapter 3 – Expansions are provided here to help students prepare and excel in their exams This chapter mainly deals with problems based on expansions Experts tutors have formulated the solutions in a step by step manner for students to grasp the concepts easily From the exam point of view, solving the problems on a regular basis,




6 Div 0 2 See How To Solve It At Qanda



4 The Binomial Theorem
View more examples » Access instant learning tools Get immediate feedback and guidance with stepbystep solutions and Wolfram Problem Generator Learn Find an answer to your question if x/y y/x = 1 then find x^3 y ^3 Yar kya hai tuja Sala Daru piya hai kya Jyada Jo Bar bar ek hi message repeat Kar Rah hai yah Bhut gussa dil wah Rah hai kya karu Iska Chal tuja bakshDesmos offers bestinclass calculators, digital math activities, and curriculum to help every student love math and love learning math



What Is The Binomial Expansion Of Math 1 X 2 Math Quora



What Is The Binomial Expansion Of Math 1 X 2 Math Quora
Graph{x^33x^29x5 1459, 1726, 856, 736} FIrst determine the interval of definition, then the behavior of first and second derivatives and the behavior of the function as \displaystyle{x}NCERT Solutions for Class 9 Maths Chapter 2 has 5 exercises The topics discussed in these exercises are polynomials in one Variable, zeros of a polynomial, real numbers and their decimal expansions, representing real numbers on the number line and operations on real numbers laws of exponents for real numbersExample Expand 3 × (52) Answer It is now expanded We can also complete the calculation 3 × (52) = 3 × 5 3 × 2 = 15 6 = 21 In Algebra In Algebra putting two things next to each other usually means to multiply So 3(ab) means to multiply 3 by (ab) Here is an example of expanding, using variables a, b and c instead of numbers




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials In Pdf



Find The Cube Of Each Of The Following Binomial Expressions I 1 X Y 3 Ii 3 X 2 X 2 Sarthaks Econnect Largest Online Education Community
Denotes the factorial of nIn the more compact sigma notation, this can be written as = ()!1 x 2 = (3 2i) x 1 x 2 )2ix 2 = x 1 For x 2 = 1 we obtain x(1) = (2i 1 Finally for the second eigenvalue 2, the eigenvector is x(2) = 2i i Math 331 Homework Assignment Chapter 7 Page 4 of 9 4 For the system of di erential equations x0= Ax A = 2 5 1 2 and the two vectorvalued functions x 1(t) = 5cost 2cost sint ; Ex 25, 4 Expand each of the following, using suitable identities (x 2y 4z)2 (x 2y 4z)2 Using (a b c)2 = a2 b2 c2 2ab 2bc 2ac Where a = x , b




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Ex 2 5 Cbsetuts Com




Number Of Terms In Expansion Of Following I 2x 3y 9 Ii 2
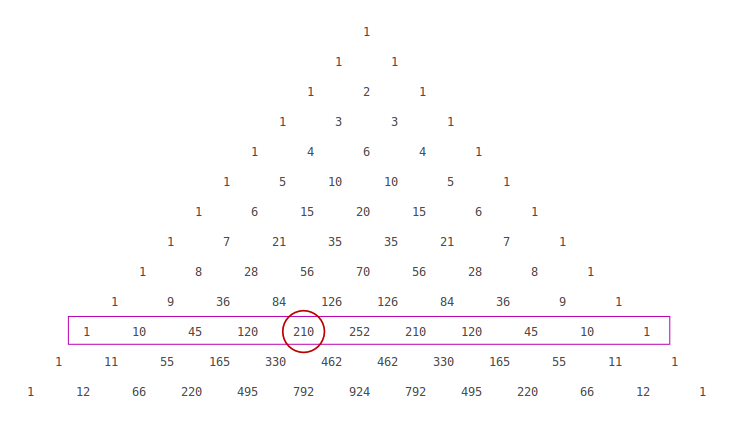
They have the same value for all values of \ (xTo generate Pascal's Triangle, we start by writing a 1 In the row below, row 2, we write two 1's In the 3 rd row, flank the ends of the rows with 1's, and add latex11/latex to find the middle number, 2 In the latexn\text{th}/latex row, flank the ends of the row with 1'sDefinition The Taylor series of a real or complexvalued function f (x) that is infinitely differentiable at a real or complex number a is the power series ′ ()!() ″ ()!() ‴ ()!() ,where n!




X 2 2y 3 1 X Y 3 3 Solve The Given Equation Using Elimination And Substitution Method Youtube




Expand 1 3 X 2 3 Y Whole Cube Brainly In
(x 1) (x − 2) (x 3) (x − 4) Apply the distributive property by multiplying each term of x1 by each term of x2 Apply the distributive property by multiplying each term of x 1 by each term of x − 2Steps for Solving Linear Equation 3x2y = 7 3 x − 2 y = 7 Add 2y to both sides Add 2 y to both sides 3x=72y 3 x = 7 2 y The equation is in standard form The equation is in standard form Question 5 Find the remainder when x 3 x 2 x 1 is divided by x – using remainder theorem Solution Let p (x) = x 3 x 2 x 1 and q (x) = x – Here, p (x) is divided by q (x) ∴ By using remainder theorem, we have Question 6 Find the common factor in the quadratic polynomials x 2 8x 15 and x 2 3x – 10




Ncert Solutions For Class 12 Maths Chapter 4 Determinants Mathongo




1 X Y 3 3 Expand Brainly In
NCERT Solutions for Class 9 Maths Chapter 4 Linear Equations In Two Variables Exercise 43 1 Draw the graph of each of the following linear equations in two variables (i) xy = 4 Solution To draw a graph of linear equations in two variables, let us find out the points to plot5 Classify the following as linear, quadratic and cubic polynomials ∵ The degree of x 2 x is 2 ∴ It is a quadratic polynomial ∵ The degree of x – x 3 is 3 ∴ It is a cubic polynomial ∵ The degree of y y 2 4 is 2 ∴ It is a quadratic polynomial ∵ The degree of 1 x is 1In mathematics, the binomial coefficients are the positive integers that occur as coefficients in the binomial theoremCommonly, a binomial coefficient is indexed by a pair of integers n ≥ k ≥ 0 and is written () It is the coefficient of the x k term in the polynomial expansion of the binomial power (1 x) n, and is given by the formula =!!()!For example, the fourth power of 1 x is




Expand 1 X Y 3 3 Novocom Top




Rd Sharma Class 9 Solutions Chapter 4 Algebraic Identities
Remainder of x^32x^25x7 divided by x3;We can skip n=0 and 1, so next is the third row of pascal's triangle 1 2 1 for n = 2 the x^2 term is the rightmost one here so we'll get 1 times the first term to the 0 power times the second term squared or 1*1^0* (x/5)^2 = x^2/25 so not here 1 3 3 1 for n = 3 Squared term is second from the right, so we get 3*1^1* (x/5)^2 = 3x^2/25 so notPolynomial Identities When we have a sum (difference) of two or three numbers to power of 2 or 3 and we need to remove the brackets we use polynomial identities (short multiplication formulas) (x y) 2 = x 2 2xy y 2 (x y) 2 = x 2 2xy y 2 Example 1 If x = 10, y = 5a (10 5a) 2 = 10 2 2·10·5a (5a) 2 = 100 100a 25a 2




Omtex Classes X Y 5 X Y 3 Solve The Following Simultaneous Equations Graphically




Rd Sharma Solutions For Class 8 Chapter 6 Algebraic Expressions And Identities Exercise 6 6 Access Free Pdf
Example 3 Find the 4th term from the end in the expansion of 3 9 2 2 2 x x − Solution Since rth term from the end in the expansion of (a b)n is (n – r 2)th term from the beginning Therefore 4 th term from the end is 9 – 4 2, ie, 7 th term from the beginning, which is given by T 7 = 3 3 6 9 6 2 2 C 2 x x − = 9 9 3 12 3 3 64 9 8 If ` (x)/(y)(y)/(x)=1`, where` x,y ne 0` then the value of `(x^3y^3)` is A 1 B 1 C 0 D `(1)/(2)` class9;Find (3 x) 3 The power that we are expanding the bracket to is 3, so we look at the third line of Pascal's triangle, which is 1 3 3 1 So the answer is 3 3 3 × (3 2 × x) 3 × (x 2 × 3) x 3 (we are replacing a by 3 and b by x in the expansion of (a b) 3 above) Generally
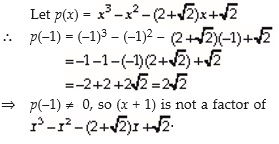



Ncert Solutions Polynomials Mathematics Class 9




X 2 2y 3 1 And X Y 3 3 Find X And Y Values Using Elimination And Substitution Method Youtube
Problems on Binomial Theorem Question 1 If the third term in the binomial expansion of equals 2560, find x Solution ⇒ (log 2x) 2 = 4 ⇒ log 2x = 2 or 2 ⇒ x = 4 or 1/4 Question 2 Find the positive value of λ for which the coefficient of x2 in the expression x2√ x Transcript Ex 25, 6 Write the following cubes in expanded form (i) (2x 1)3 (2x 1)3 Using (a b)3 = a3 b3 3ab(a b) Where a = 2x & b =1 = (2x)3 (1)3 3(2x)(1) (2x 1) = 8x3 1 6x(2x 1) = 8x3 1 12x2 6x = 8x3 12x2 6x 1 Ex 25, 6 Write the following cubes in expanded form (ii) (2a 3b)3 (2a 3b)3 Using (x y)3 = x3 y3 3xy(x y) Where x = 2a & y = 3b = (2a)39x=09 to the power of x equals 0Take the log of both sides log10 (9x)=log10 (0) Rewrite the left side of the equation using the rule for the log of a power x•log10 (9)=log10 (0) Isolate the variable x ax26xa2=0 No solutions found Step by step solution Step 1 Equation at the end of step 1 ax2 a 6x 2 = 0 Step 2 Solving a




Selina Mathematics Class 9th Solutions Icse Chapter 4 Expansion




6 Div 0 2 See How To Solve It At Qanda
Y = 3 x 4 Arithmetic 699 * 533 6 9 9 { 1 } x e ^ { x ^ { 2 } } d x Algebra Combine Like Terms Solve for a Variable Factor Expand Evaluate Fractions Linear Equations Quadratic Equations Inequalities Systems of Equations Matrices Trigonometry Simplify Evaluate Graphs Solve Equations CalculusIn elementary algebra, the binomial theorem (or binomial expansion) describes the algebraic expansion of powers of a binomialAccording to the theorem, it is possible to expand the polynomial (x y) n into a sum involving terms of the form ax b y c, where the exponents b and c are nonnegative integers with b c = n, and the coefficient a of each term is a specific positiveStandard Form of a Decimal Number In Britain this is another name for Scientific Notation, where you write down a number this way In this example, is written as × 10 3, because = × 1000 = × 10 3 In other countries it means "not in expanded form" (see Composing and Decomposing Numbers)




Partial Fraction Expansion Video Khan Academy




Please Expand 1 X Y 3 Whole Cube Brainly In
QuickMath will automatically answer the most common problems in algebra, equations and calculus faced by highschool and college students The algebra section allows you to expand, factor or simplify virtually any expression you choose It also has commands for splitting fractions into partial fractions, combining several fractions into one and = x 3 1 x 2 x = (iv) (x − y) 3 Solution Using formula, (x – y) 3 = x 3 – y 3 – 3xy(x – y) (x − y) 3 = x 3 − y 3 – 3(x) yx − y = x 3 – y 3 – 2x 2 y xy 2 Question 7 Evaluate the following using suitable identities (i) (99) 3 Solution 99 = 100 – 1Eg, since 1000 = 10 × 10 × 10 = 10 3, the "logarithm base




Selina Solutions Class 9 Concise Maths Chapter 5 Factorisation Download Free Pdf
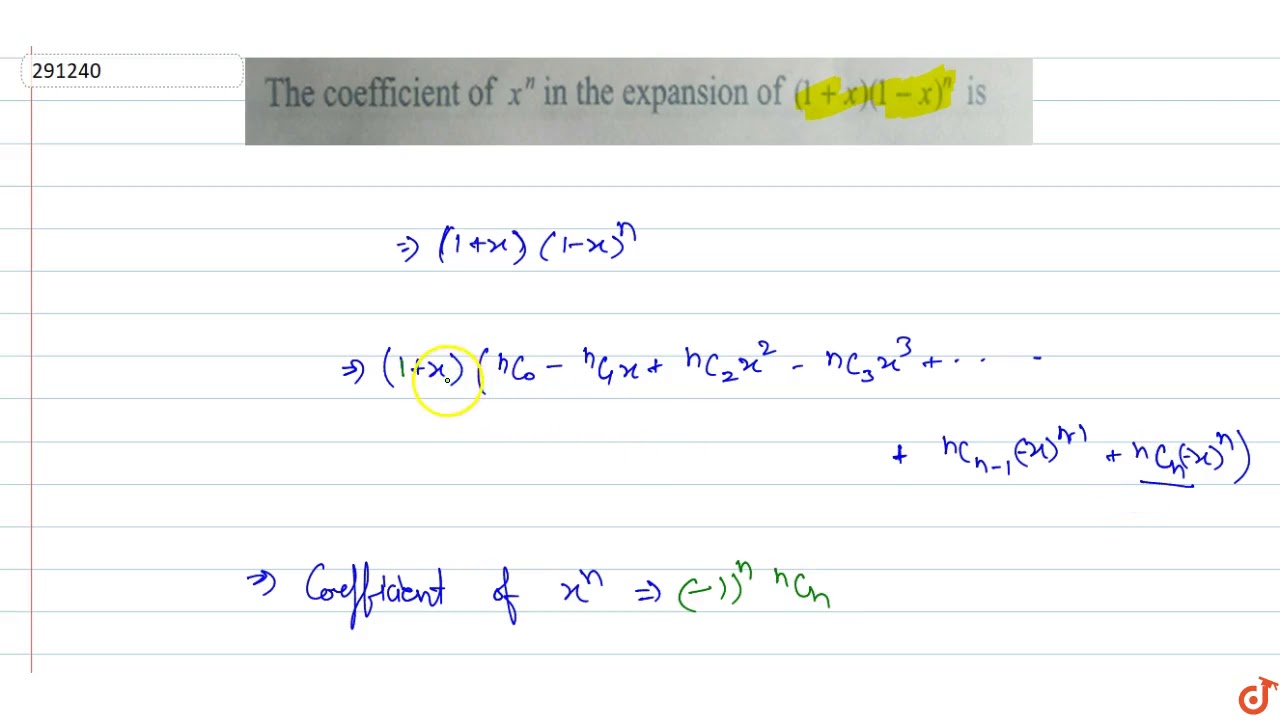



The Coefficient Of X N In The Expansion Of 1 X 1 X N Is Youtube
Factorisation is the opposite process of expanding brackets For example, expanding brackets would require \ (2 (x 1)\) to be written as \ (2x 2\) Factorisation would be to start with \ (2x 2\) and end up with \ (2 (x 1)\) The two expressions \ (2 (x 1)\) and \ (2x2\) are equivalent;Expand polynomial (x3)(x^35x2) GCD of x^42x^39x^246x16 with x^48x^325x^246x16;Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history




Ml Aggarwal Icse Solutions For Class 9 Maths Chapter 4 Factorisation Icse Solutions




If X 3 A N D Y 1 Find The Values Of Each Of The Using Identi
Steps for Solving Linear Equation 3x4y=3 3 x − 4 y = 3 Add 4y to both sides Add 4 y to both sides 3x=34y 3 x = 3 4 y The equation is in standard form The equation is in standard formThe Binomial theorem tells us how to expand expressions of the form (ab)ⁿ, for example, (xy)⁷ The larger the power is, the harder it is to expand expressions like this directly But with the Binomial theorem, the process is relatively fast!Suppose we want to expand (2xy)3 We pick the coefficients in the expansion from the relevant row of Pascal's triangle (1,3,3,1) As we move through the terms in the expansion from left to right we remember to decrease the power of 2x and increase the power of y So, (2xy)3 = 1(2x)3 3(2x)2y 3(2x)1y2 1y3 = 8x3 12x 2y 6xy y3 Example




Chapter 8 Binomial Theorem




Qg0dbobeox2fsm
Ex 32, 11 If x 8(2@3) y 8(−1@1) = 8(10@5) , find values of x and y x 8(2@3) y 8(−1@1) = 8(10@5) 8(2𝑥@3𝑥) 8(−𝑦@𝑦



What Is The Answer Of X Y Quora




Selina Concise Mathematics Class 9 Icse Solutions For Chapter 3 Expansions




Ex 2 5 6 Write The Following Cubes In Expanded Form Ex 2 5




Binomial Theorem Concept And Applications Handa Ka Funda Online Coaching For Cat And Banking Exams
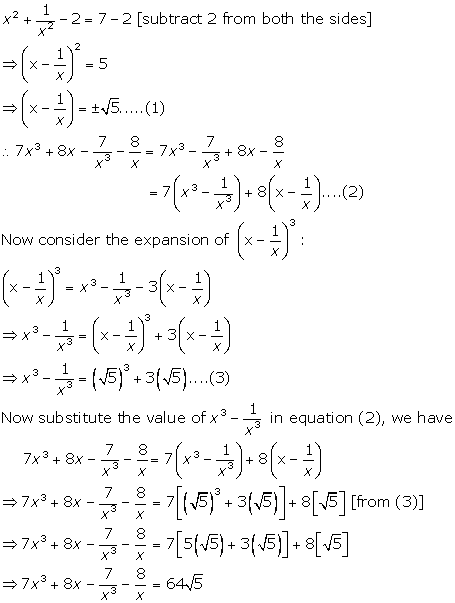



Chapter 4 Expansion Selina Concise Mathematics Part I Solutions For Class 9 Mathematics Icse Topperlearning




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Ex 2 5 Cbsetuts Com
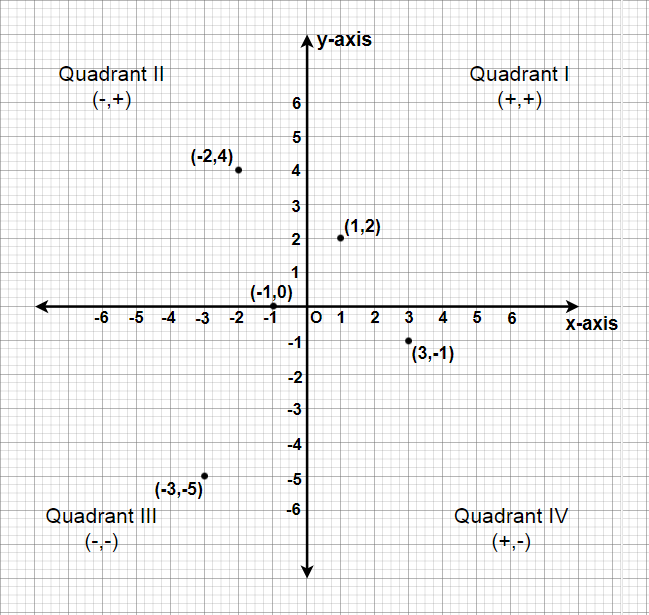



Class 9 Ncert Solutions Chapter 3 Coordinate Geometry Exercise 3 3 Geeksforgeeks




Kseeb Solutions For Class 9 Maths Chapter 4 Polynomials Ex 4 5 Kseeb Solutions




Ncert Solutions For Class 9 Maths Chapter 2 Exercise 2 5 Polynomials
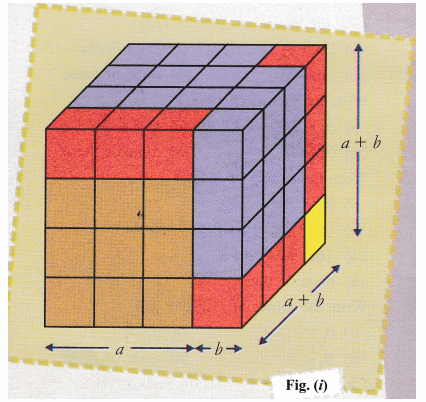



Cbse Class 9 Maths Lab Manual Algebraic Identity A B 3 A3 3a2b 3ab2



Expand 1 X Y 3 Whole Cube Studyrankersonline
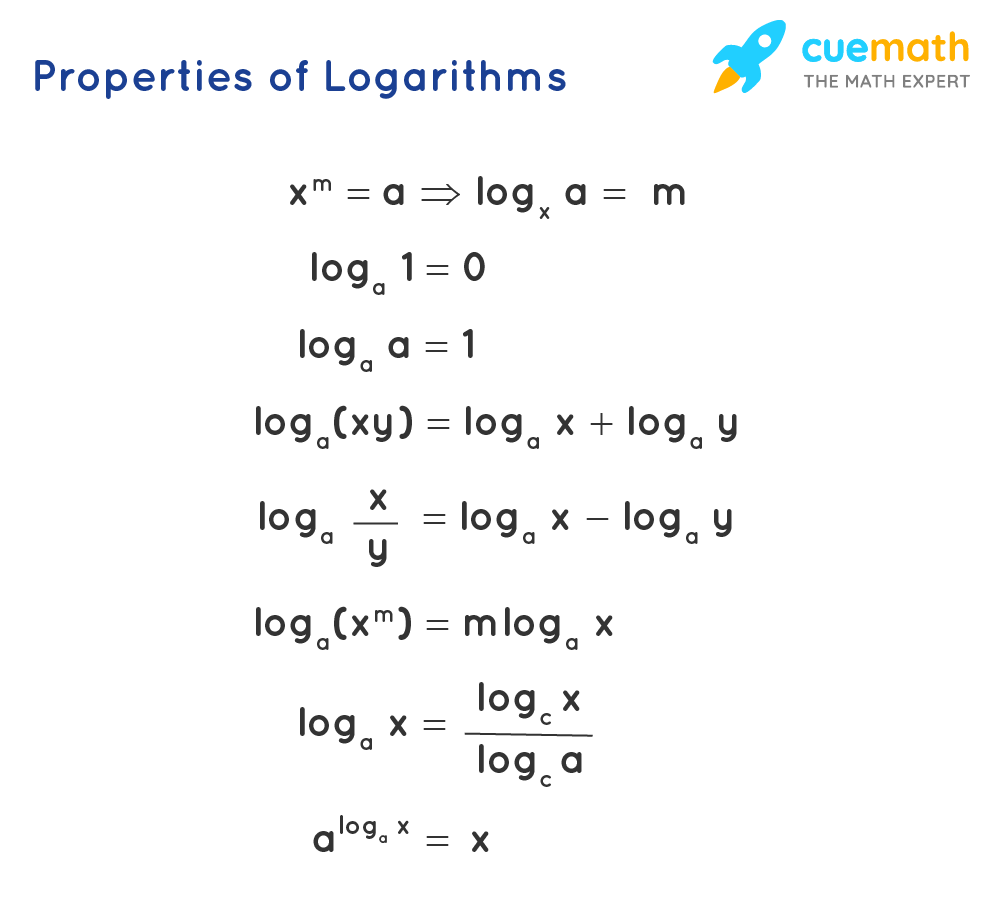



Algebra Formula Solved Examples List Of Algebraic Formulas




Expanding Binomials Video Polynomials Khan Academy




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials In Pdf
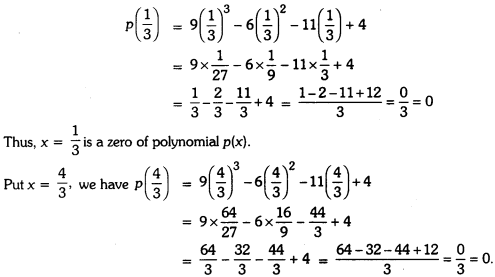



Polynomials Class 9 Extra Questions Maths Chapter 2 With Solutions Answers




Hc1lhhvxiawfym
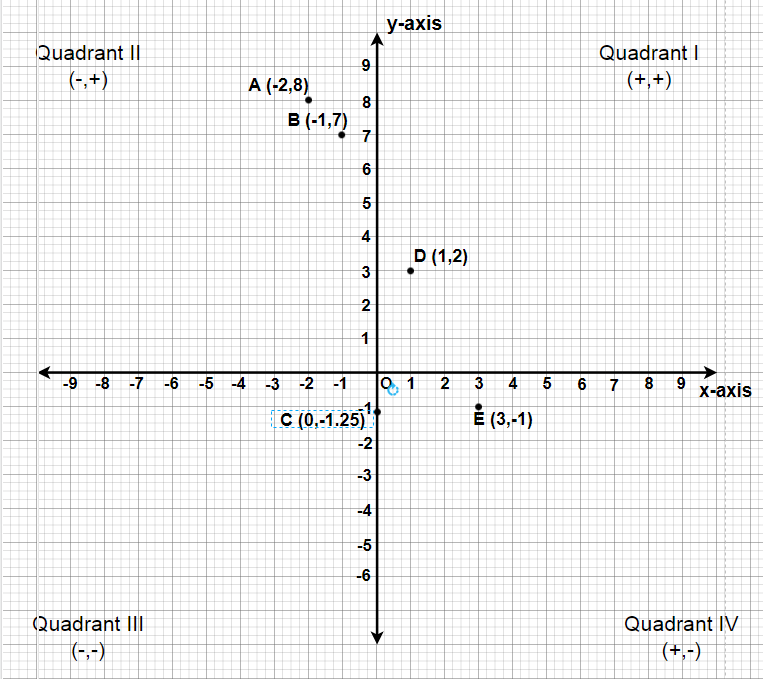



Class 9 Ncert Solutions Chapter 3 Coordinate Geometry Exercise 3 3 Geeksforgeeks



Evaluate 104 Cube Using A Suitable Identity Studyrankersonline




Ml Aggarwal Solutions For Class 9 Chapter 3 Expansions Download Free Pdf




Rd Sharma Class 9th Solutions Chapter 1 Number Systems




Kseeb Solutions For Class 9 Maths Chapter 4 Polynomials Ex 4 5 Kseeb Solutions




Expansions Popular Questions Icse Class 9 Math Mathematics Meritnation
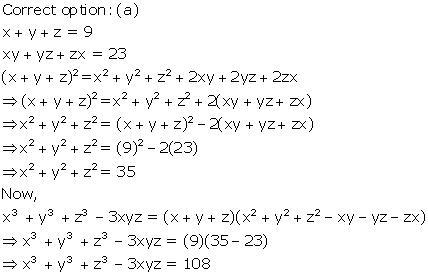



Chapter 3 Factorisation Of Polynomials R S Aggarwal And V Aggarwal Solutions For Class 9 Mathematics Cbse Topperlearning
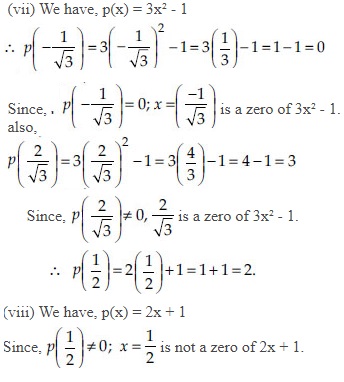



Ncert Solutions Polynomials Mathematics Class 9
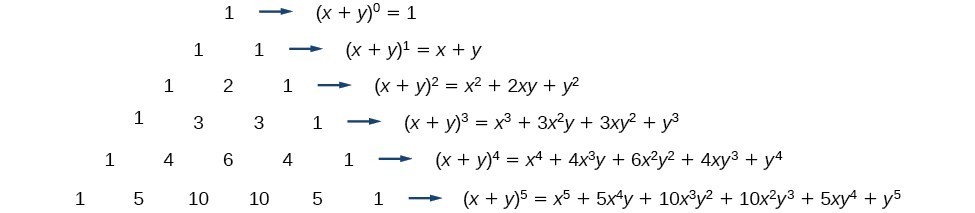



Use The Binomial Theorem College Algebra




Notes Of Ch 2 Polynomials Class 9th Math




Mp Board Class 9th Maths Solutions Chapter 2 Polynomials Ex 2 5 Mp Board Solutions




Algebraic Identities Of Polynomials A Plus Topper



Ambiguous Pemdas




Ex 2 5 6 Write The Following Cubes In Expanded Form Ex 2 5




Ncert Solutions For Class 9 Maths Chapter 2 Exercise 2 5 Polynomials




Videos And Worksheets Corbettmaths



1




Expand 1 X Y 3 3 Solve It Fastly Brainly In




Expand 1x Y3 3 Maths Questions



Which Term In The Expansion Of X Y 1 3 Y X 1 3 1 2 21 Contains X And Y To One And The Same Power Sarthaks Econnect Largest Online Education Community



Mrurbanc Weebly Com Uploads 4 4 2 6 Pages From Hl Exam Review Assignment Answers Part 1 Pages 01 Pdf




Factorisation Algebraic Expressions Siyavula
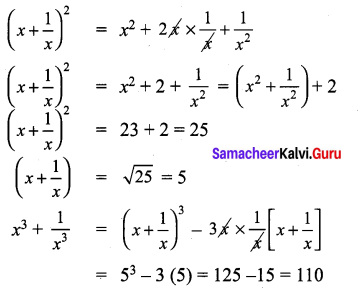



Samacheer Kalvi 9th Maths Solutions Chapter 3 Algebra Ex 3 4 Samacheer Kalvi



Cbse 9 Math Cbse Polynomials Ncert Solutions




The Coefficient Of X 10 In The Expansion Of 1 X 2 1 X 2 3 1 X 3 4 Is Equal To




Ml Aggarwal Icse Solutions For Class 9 Maths Ch 3 Expansions A Plus Topper



How Do You Find The Coefficient Of X 6 In The Expansion Of 2x 3 10 Socratic




Ex 8 2 8 Find Middle Terms Of X 3 9y 10 Binomial




Expand Each Of The Following Using Suitable Identities 2x 3y 2z 2



Kumarsir34 Files Wordpress Com 21 02 Maths Class X Sample Test Paper 08 For Board Exam 21 Answers Pdf




Example 10 Find Term Independent Of X In 3 2 X 2 1 3x 6




Mp Board Class 9th Maths Solutions Chapter 2 Polynomials Ex 2 5 Mp Board Solutions




Ex 2 5 6 Write The Following Cubes In Expanded Form Ex 2 5




Taylor Mclaurin Series Questions And Answers Sanfoundry




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials



1




Find The Coefficient Of X 6y 3in The Expansion Of X 2y 9
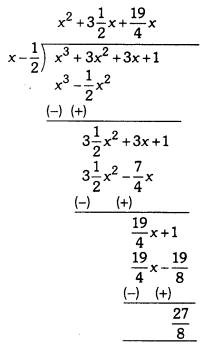



Polynomials Class 9 Extra Questions Maths Chapter 2 With Solutions Answers




Notes Of Ch 2 Polynomials Class 9th Math




Expand 1 X Y 3 3 Novocom Top



Q Tbn And9gcqw3ytr8shmxjcu2 37v8gqgdbytzhzbbgxwcuepfumanvsy3e4 Usqp Cau



1




Expand 1 X Y 3 3 Novocom Top




Use The Binomial Theorem College Algebra




Taylor Series Wikipedia




Important Questions For Cbse Class 9 Maths Chapter 2 Polynomials




Ml Aggarwal Solutions For Class 9 Chapter 3 Expansions Download Free Pdf




Algebraic Identities Of Polynomials A Plus Topper




Binomial Theorem Wikipedia




Exponent Rules 7 Key Strategies To Solve Tough Equations Prodigy Education




Expand 1x Y3 3 Maths Questions




Expand Each Of The Following Using Suitable Identities I X 2y 4z 2 Ii 2x Y Z Youtube




Expansions Popular Questions Icse Class 9 Math Mathematics Meritnation



Cbse 9 Math Cbse Polynomials Ncert Solutions
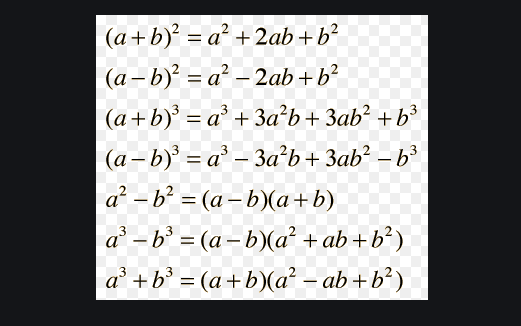



Expansions Ml Aggarwal Icse Class 9 Maths Solutions Icsehelp




Algebra Formulas For Class 9 Pdf Download Free Here
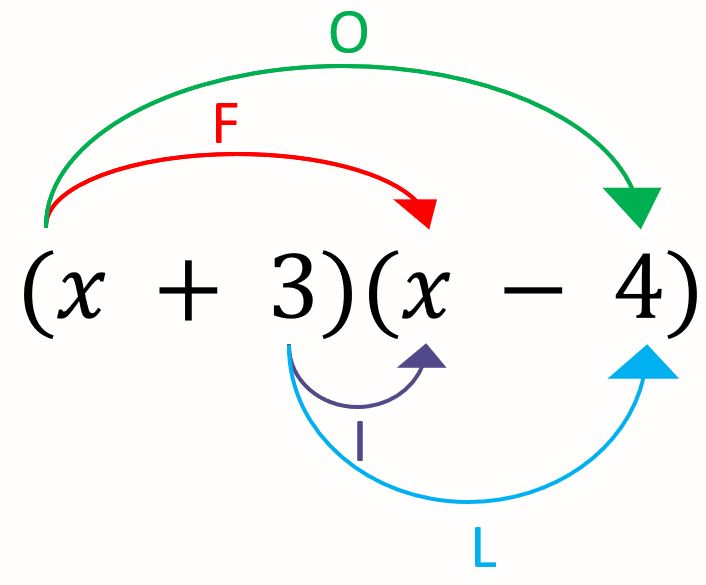



Expanding Brackets Worksheets Multiplying Out Brackets Mme




Section 9 Binomial Expansion Questions About Homework Submit Homework Recall The Exercises We Did Last Class 04 01 19 Math 106 Section 9 1 Slideshow And Powerpoint Viewer What Is Binomi



No comments:
Post a Comment